Integer Programming in Python

I am going to solve a problem with integer programming in this tutorial. Integer programming (IP) is an optimization method that is restricted to use integer variables, variables with binary values (0 and 1) is common in IP-problems. Integer Programming is a form of linear programming that can be used when variables represents decisions, when we want to know if we should take certain decisions or not (Yes/No).

IP is used for scheduling, assignments and decision making. Integer programming assumes that a problem can be represented as a matematical model with linear relationships. A IP-problem is represented with an objective function, variables that can be modified and constraints. I am using Python and the pulp library in this tutorial.

Capital Budgeting

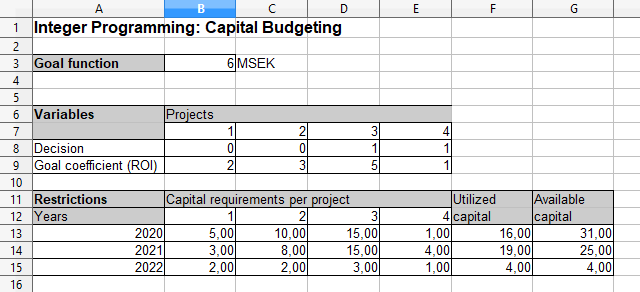
A company has identified 4 different projects as possible investments, they know the possible returns and the capital requirements for each project. Each project takes 3 years to complete but the company does not have an unlimited amount of capital to invest. The goal is to maximize the total return on investments given capital constraints.

I have created and solved the problem in OpenOffice Calc. The best solution is to go through with project 3 and 4, this gives a total return on investments of 6 MSEK.

Code

The code below shows an implementation of an integer programming solution to a capital budgeting problem. The problem is created and solved with pulp, output from a run is shown below the code.

# Import libraries
import pulp

# The main entry point for this module
def main():
    
    # Create a problem
    # Either LpMinimize (default) or LpMaximize
    problem = pulp.LpProblem('Capital-Budgeting', pulp.LpMaximize)

    # Projects
    projects = ['1', '2', '3', '4']

    # Return on investments (MSEK)
    roi = {'1':2, '2':3, '3':5, '4':1}

    # Capital requirments (MSEK)
    y2020 = {'1':5, '2':10, '3':15, '4':1}
    y2021 = {'1':3, '2':8, '3':15, '4':4}
    y2022 = {'1':2, '2':2, '3':3, '4':1}

    # Create decision variables (values that can be modified by solver)
    # Category: Integer, Binary or Continuous(default)
    decision = pulp.LpVariable.dicts('Project', projects, lowBound=None, upBound=None, cat='Binary')

    # Objective function
    problem += pulp.lpSum([roi[i] * decision[i] for i in projects])

    # Constraints
    problem += pulp.lpSum([y2020[i] * decision[i] for i in projects]) <= 31
    problem += pulp.lpSum([y2021[i] * decision[i] for i in projects]) <= 25
    problem += pulp.lpSum([y2022[i] * decision[i] for i in projects]) <= 4
    
    # Print problem
    print(problem)

    # Write problem data to an .lp file
    problem.writeLP('plots\\capital_budgeting.lp')

    # Solve the problem by using PuLP's choice of Solver
    problem.solve()

    # Print the status of the solution
    print('Status: {0}\n'.format(pulp.LpStatus[problem.status]))

    # Print each variable with optimal value
    print('Decisions')
    for v in problem.variables():
        print(v.name, "=", v.varValue)
    print()

    # Print the optimal goal value
    print('Total Return On Investments (MSEK) = {0}\n'.format(pulp.value(problem.objective)))

# Tell python to run main method
if __name__ == '__main__': main()

Output

Capital-Budgeting:
MAXIMIZE
2*Project_1 + 3*Project_2 + 5*Project_3 + 1*Project_4 + 0
SUBJECT TO
_C1: 5 Project_1 + 10 Project_2 + 15 Project_3 + Project_4 <= 31

_C2: 3 Project_1 + 8 Project_2 + 15 Project_3 + 4 Project_4 <= 25

_C3: 2 Project_1 + 2 Project_2 + 3 Project_3 + Project_4 <= 4

VARIABLES
0 <= Project_1 <= 1 Integer
0 <= Project_2 <= 1 Integer
0 <= Project_3 <= 1 Integer
0 <= Project_4 <= 1 Integer

Status: Optimal

Decisions
Project_1 = 0.0
Project_2 = 0.0
Project_3 = 1.0
Project_4 = 1.0

Total Return On Investments (MSEK) = 6.0