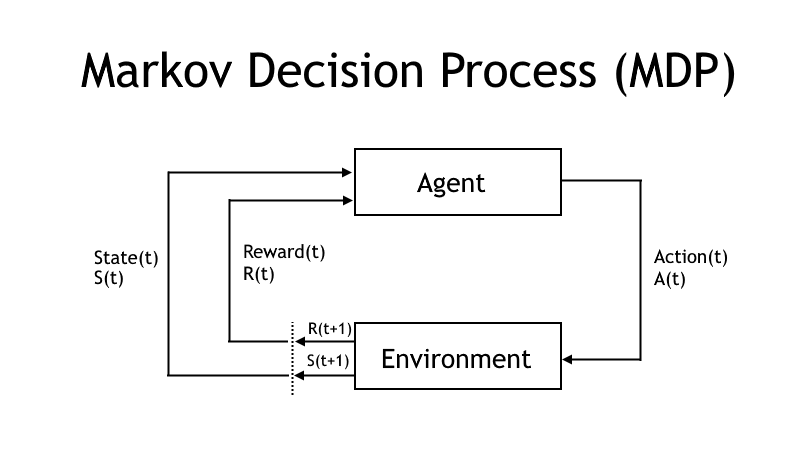
I will apply adaptive dynamic programming (ADP) in this tutorial, to learn an agent to walk from a point to a goal over a frozen lake. ADP is a form of passive reinforcement learning that can be used in fully observable environments. Adaptive dynamic programming learns the best markov decision process (MDP) policy to be applied to a problem in a known world.
Adaptive dynamic programming is an optimization algorithm that learns the best policy of actions to be performed by using policy/value iteration and policy improvement. ADP uses probability tables for transitions between states and utility estimates to find the best sequence of actions to perform in order to solve a problem.
ADP will find an optimal solution in a fully observable environment but it will not be possible to apply the algorithm in large state spaces, it will take to much time to solve all the equations in large state spaces. A discount factor (gamma) and a convergence (theta) value is used to find the best policy/model. The theta value is a very small positive value that indicates if the estimate has converged to the true value. The discount factor determines how important future rewards is, a discount factor of 0 means that current rewards is most important while a discount factor of 1 means that a long-time reward is most important.
Problem and Libraries
An agent should learn how to walk from a starting point to a goal point over a frozen lake with holes and a slippery ground. The agent is rewarded 1 point if he reaches the goal and 0 points otherwise, the game is over if the agent reaches the goal or if he falls into a hole. The agent can move left, down, right or up. The movement direction is uncertain because of the slippery ground. The frozen lake problem is part of the gym library, i am also using the following libraries: os, random, copy, pickle, numpy and matplotlib.
Red Marker in Command Prompt
You need to add VirtualTerminalLevel and a value of 1 in the registry editor in HKEY_CURRENT_USER\Console if you want the red marker to show up in the command prompt on Windows 10.
Code
The full code is shown below, it includes 4 different methods to approach the problem. It is possible to save and load models with pickle. A random policy does not involve any learning at all and it will show the worst case scenario.
# Import libraries
import os
import random
import gym
import copy
import pickle
import numpy as np
import matplotlib.pyplot as plt
# Plot values
# https://github.com/xadahiya/frozen-lake-dp-rl/blob/master/Dynamic_Programming_Solution.ipynb
def plot_values(V):
# reshape value function
V_sq = np.reshape(V, (8,8))
# plot the state-value function
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111)
im = ax.imshow(V_sq, cmap='cool')
for (j,i),label in np.ndenumerate(V_sq):
ax.text(i, j, np.round(label, 5), ha='center', va='center', fontsize=12)
plt.tick_params(bottom='off', left='off', labelbottom='off', labelleft='off')
plt.title('State-Value Function')
plt.show()
# Perform a policy evaluation
# https://github.com/xadahiya/frozen-lake-dp-rl/blob/master/Dynamic_Programming_Solution.ipynb
def policy_evaluation(env, policy, gamma=1, theta=1e-8):
V = np.zeros(env.nS)
while True:
delta = 0
for s in range(env.nS):
Vs = 0
for a, action_prob in enumerate(policy[s]):
for prob, next_state, reward, done in env.P[s][a]:
Vs += action_prob * prob * (reward + gamma * V[next_state])
delta = max(delta, np.abs(V[s]-Vs))
V[s] = Vs
if delta < theta:
break
return V
# Perform policy improvement
# https://github.com/xadahiya/frozen-lake-dp-rl/blob/master/Dynamic_Programming_Solution.ipynb
def policy_improvement(env, V, gamma=1):
policy = np.zeros([env.nS, env.nA]) / env.nA
for s in range(env.nS):
q = q_from_v(env, V, s, gamma)
# OPTION 1: construct a deterministic policy
# policy[s][np.argmax(q)] = 1
# OPTION 2: construct a stochastic policy that puts equal probability on maximizing actions
best_a = np.argwhere(q==np.max(q)).flatten()
policy[s] = np.sum([np.eye(env.nA)[i] for i in best_a], axis=0)/len(best_a)
return policy
# Obtain q from V
# https://github.com/xadahiya/frozen-lake-dp-rl/blob/master/Dynamic_Programming_Solution.ipynb
def q_from_v(env, V, s, gamma=1):
q = np.zeros(env.nA)
for a in range(env.nA):
for prob, next_state, reward, done in env.P[s][a]:
q[a] += prob * (reward + gamma * V[next_state])
return q
# Perform policy iteration
# https://github.com/xadahiya/frozen-lake-dp-rl/blob/master/Dynamic_Programming_Solution.ipynb
def policy_iteration(env, gamma=1, theta=1e-8):
policy = np.ones([env.nS, env.nA]) / env.nA
while True:
V = policy_evaluation(env, policy, gamma, theta)
new_policy = policy_improvement(env, V)
# OPTION 1: stop if the policy is unchanged after an improvement step
if (new_policy == policy).all():
break;
# OPTION 2: stop if the value function estimates for successive policies has converged
# if np.max(abs(policy_evaluation(env, policy) - policy_evaluation(env, new_policy))) < theta*1e2:
# break;
policy = copy.copy(new_policy)
return policy, V
# Truncated policy evaluation
# https://github.com/xadahiya/frozen-lake-dp-rl/blob/master/Dynamic_Programming_Solution.ipynb
def truncated_policy_evaluation(env, policy, V, max_it=1, gamma=1):
num_it=0
while num_it < max_it:
for s in range(env.nS):
v = 0
q = q_from_v(env, V, s, gamma)
for a, action_prob in enumerate(policy[s]):
v += action_prob * q[a]
V[s] = v
num_it += 1
return V
# Truncated policy iteration
# https://github.com/xadahiya/frozen-lake-dp-rl/blob/master/Dynamic_Programming_Solution.ipynb
def truncated_policy_iteration(env, max_it=1, gamma=1, theta=1e-8):
V = np.zeros(env.nS)
policy = np.zeros([env.nS, env.nA]) / env.nA
while True:
policy = policy_improvement(env, V)
old_V = copy.copy(V)
V = truncated_policy_evaluation(env, policy, V, max_it, gamma)
if max(abs(V-old_V)) < theta:
break;
return policy, V
# Value iteration
# https://github.com/xadahiya/frozen-lake-dp-rl/blob/master/Dynamic_Programming_Solution.ipynb
def value_iteration(env, gamma=1, theta=1e-8):
V = np.zeros(env.nS)
while True:
delta = 0
for s in range(env.nS):
v = V[s]
V[s] = max(q_from_v(env, V, s, gamma))
delta = max(delta,abs(V[s]-v))
if delta < theta:
break
policy = policy_improvement(env, V, gamma)
return policy, V
# Get an action (0:Left, 1:Down, 2:Right, 3:Up)
def get_action(model, state):
return np.random.choice(range(4), p=model[state])
# Save a model
def save_model(bundle:(), type:str):
with open('models\\frozen_lake' + type + '.adp', 'wb') as fp:
pickle.dump(bundle, fp)
# Load a model
def load_model(type:str) -> ():
if(os.path.isfile('models\\frozen_lake' + type + '.adp') == True):
with open ('models\\frozen_lake' + type + '.adp', 'rb') as fp:
return pickle.load(fp)
else:
return (None, None)
# The main entry point for this module
def main():
# Create an environment
env = gym.make('FrozenLake8x8-v0', is_slippery=True)
# Print information about the problem
print('--- Frozen Lake ---')
print('Observation space: {0}'.format(env.observation_space))
print('Action space: {0}'.format(env.action_space))
print()
# Print one-step dynamics (probability, next_state, reward, done)
print('--- One-step dynamics')
print(env.P[1][0])
print()
# (1) Random policy
#model, V = load_model('1')
model = np.ones([env.nS, env.nA]) / env.nA
V = policy_evaluation(env, model)
print('Optimal Policy (LEFT = 0, DOWN = 1, RIGHT = 2, UP = 3):')
print(model,'\n')
plot_values(V)
save_model((model, V), '1')
# (2) Policy iteration
##model, V = load_model('2')
#model, V = policy_iteration(env)
#print('Optimal Policy (LEFT = 0, DOWN = 1, RIGHT = 2, UP = 3):')
#print(model,'\n')
#plot_values(V)
#save_model((model, V), '2')
# (3) Truncated policy iteration
##model, V = load_model('3')
#model, V = truncated_policy_iteration(env, max_it=2)
#print('Optimal Policy (LEFT = 0, DOWN = 1, RIGHT = 2, UP = 3):')
#print(model,'\n')
#plot_values(V)
#save_model((model, V), '3')
# (4) Value iteration
##model, V = load_model('4')
#model, V = value_iteration(env)
#print('Optimal Policy (LEFT = 0, DOWN = 1, RIGHT = 2, UP = 3):')
#print(model,'\n')
#plot_values(V)
#save_model((model, V), '4')
# Variables
episodes = 10
timesteps = 200
total_score = 0
# Loop episodes
for episode in range(episodes):
# Start episode and get initial observation
state = env.reset()
# Reset score
score = 0
# Loop timesteps
for t in range(timesteps):
# Get an action (0:Left, 1:Down, 2:Right, 3:Up)
action = get_action(model, state)
# Perform a step
# Observation (position, reward: 0/1, done: True/False, info: Probability)
state, reward, done, info = env.step(action)
# Update score
score += reward
total_score += reward
# Check if we are done (game over)
if done:
# Render the map
print('--- Episode {} ---'.format(episode+1))
env.render(mode='human')
print('Score: {0}, Timesteps: {1}'.format(score, t+1))
print()
break
# Close the environment
env.close()
# Print the score
print('--- Evaluation ---')
print ('Score: {0} / {1}'.format(total_score, episodes))
print()
# Tell python to run main method
if __name__ == "__main__": main()Random Policy
--- Frozen Lake ---
Observation space: Discrete(64)
Action space: Discrete(4)
--- One-step dynamics
[(0.3333333333333333, 1, 0.0, False), (0.3333333333333333, 0, 0.0, False), (0.3333333333333333, 9, 0.0, False)]
Optimal Policy (LEFT = 0, DOWN = 1, RIGHT = 2, UP = 3):
[[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]]
--- Episode 1 ---
(Down)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 10
--- Episode 2 ---
(Down)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 75
--- Episode 3 ---
(Up)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 28
--- Episode 4 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 20
--- Episode 5 ---
(Down)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 8
--- Episode 6 ---
(Left)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 51
--- Episode 7 ---
(Up)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 19
--- Episode 8 ---
(Down)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 26
--- Episode 9 ---
(Left)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 24
--- Episode 10 ---
(Down)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 31
--- Evaluation ---
Score: 0.0 / 10Policy Iteration
--- Frozen Lake ---
Observation space: Discrete(64)
Action space: Discrete(4)
--- One-step dynamics
[(0.3333333333333333, 1, 0.0, False), (0.3333333333333333, 0, 0.0, False), (0.3333333333333333, 9, 0.0, False)]
Optimal Policy (LEFT = 0, DOWN = 1, RIGHT = 2, UP = 3):
[[0. 0.5 0.5 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[0. 0.5 0. 0.5 ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0. 0. 0. 1. ]
[0.5 0. 0. 0.5 ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[0. 1. 0. 0. ]
[0. 0. 0. 1. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0. 0.5 0.5 0. ]
[0. 0. 0. 1. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0.5 0.5 0. ]
[0.5 0. 0. 0.5 ]
[0.25 0.25 0.25 0.25]
[0.5 0. 0.5 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0. 1. 0. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0.5 0.5 0. ]
[0. 0. 1. 0. ]
[0. 1. 0. 0. ]
[0.25 0.25 0.25 0.25]]
--- Episode 1 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 36
--- Episode 2 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 169
--- Episode 3 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 113
--- Episode 4 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 94
--- Episode 5 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 66
--- Episode 6 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 111
--- Episode 7 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 132
--- Episode 8 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 40
--- Episode 9 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 111
--- Episode 10 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 116
--- Evaluation ---
Score: 10.0 / 10Truncated Policy Iteration
--- Frozen Lake ---
Observation space: Discrete(64)
Action space: Discrete(4)
--- One-step dynamics
[(0.3333333333333333, 1, 0.0, False), (0.3333333333333333, 0, 0.0, False), (0.3333333333333333, 9, 0.0, False)]
Optimal Policy (LEFT = 0, DOWN = 1, RIGHT = 2, UP = 3):
[[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[0. 0.5 0. 0.5 ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0. 0. 0. 1. ]
[0.5 0. 0. 0.5 ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[0. 1. 0. 0. ]
[0. 0. 0. 1. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0. 0.5 0.5 0. ]
[0. 0. 0. 1. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0.5 0.5 0. ]
[0.5 0. 0. 0.5 ]
[0.25 0.25 0.25 0.25]
[0.5 0. 0.5 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0. 1. 0. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0.5 0.5 0. ]
[0. 0. 1. 0. ]
[0. 1. 0. 0. ]
[0.25 0.25 0.25 0.25]]
--- Episode 1 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 52
--- Episode 2 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 97
--- Episode 3 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 127
--- Episode 4 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 113
--- Episode 5 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 44
--- Episode 6 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 166
--- Episode 7 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 42
--- Episode 8 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 170
--- Episode 9 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 75
--- Episode 10 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 57
--- Evaluation ---
Score: 10.0 / 10Value Iteration
--- Frozen Lake ---
Observation space: Discrete(64)
Action space: Discrete(4)
--- One-step dynamics
[(0.3333333333333333, 1, 0.0, False), (0.3333333333333333, 0, 0.0, False), (0.3333333333333333, 9, 0.0, False)]
Optimal Policy (LEFT = 0, DOWN = 1, RIGHT = 2, UP = 3):
[[0. 1. 0. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[0. 0.5 0. 0.5 ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0. 0. 0. 1. ]
[0.5 0. 0. 0.5 ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[0. 1. 0. 0. ]
[0. 0. 0. 1. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0. 0.5 0.5 0. ]
[0. 0. 0. 1. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0.5 0.5 0. ]
[0.5 0. 0. 0.5 ]
[0.25 0.25 0.25 0.25]
[0.5 0. 0.5 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0. 1. 0. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0.5 0.5 0. ]
[0. 0. 1. 0. ]
[0. 1. 0. 0. ]
[0.25 0.25 0.25 0.25]]
--- Episode 1 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 96
--- Episode 2 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 116
--- Episode 3 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 188
--- Episode 4 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 124
--- Episode 5 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 200
--- Episode 6 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 71
--- Episode 7 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 90
--- Episode 8 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 102
--- Episode 9 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 52
--- Episode 10 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 200
--- Evaluation ---
Score: 8.0 / 10